Initial engagement, and seeing the first light
Several years ago - in an idle moment - I wondered (not knowing if there was already a known answer) what happens if one divides the residues of a prime p into three equi-numerous sets (that requires, of course, that p leaves remainder 1 on division by 3; as I have already remarked there are an infinite number of such primes: 7, 13, 19, 31, 37, 43, 61, 67, 73, 79, ... ). Suppose, for example, that p = 19: how do the residues in the three sets
{1, 2, 3, 4, 5, 6}, {7, 8, 9, 10, 11, 12} and {13, 14, 15, 16, 17, 18}
(forming mod p products, of course, in the manner of Wilson and Lagrange) relate to each other?
Without any calculations being performed one knows that the two outer sets are trivially related (simply because
![]() (mod 19),
(mod 19),
![]() (mod 19), ... ,
(mod 19), ... ,
![]() (mod 19)). Thus one immediately has:
(mod 19)). Thus one immediately has:
1*2*3*4*5*6 = 13*14*15*16*17*18 (mod 19)
But what of the product (mod 19) of the residues in the middle range of residues? Well, we have to calculate (I am not doing so in the most efficient way - certainly for the purposes of later work - and since my only intention at this point is simply to illustrate, then I even show the entirely redundant third product):
>
PROD1(19) := 1*2*3*4*5*6;
PROD1(19) mod 19;
![]()
![]()
>
PROD2(19) := 7*8*9*10*11*12;
PROD2(19) mod 19;
![]()
![]()
>
PROD3(19) := 13*14*15*16*17*18;
PROD3(19) mod 19;
![]()
![]()
>
Thus, while the
two outer ones
(trivially) have congruent products, the
inner one
goes its own way (as it were), in that it is
neither
'17'
nor
'2' (which would be congruent to
![]() mod 19). Of course the inner one is
not independent
of the other two, since by Wilson's theorem the product of all three sets of residues is -1 mod 19:
mod 19). Of course the inner one is
not independent
of the other two, since by Wilson's theorem the product of all three sets of residues is -1 mod 19:
> PROD1(19)*PROD2(19)*PROD3(19) mod 19;
![]()
> mods(PROD1(19)*PROD2(19)*PROD3(19), 19);
![]()
>
Now, though, I move out a bit to the example p = 61 (once again I am not interested here in fancy footwork - that will come later - I want only to demonstrate ):
>
PROD1(61) := 1*2*3*4*5*6*7*8*9*10*11*12*13*14*15*16*17*18*19*20;
PROD1(61) mod 61;
![]()
![]()
>
PROD2(61) := 21*22*23*24*25*26*27*28*29*30*31*32*33*34*35*36*37*38*39*40;
PROD2(61) mod 61;
![]()
![]()
>
PROD3(61) := 41*42*43*44*45*46*47*48*49*50*51*52*53*54*55*56*57*58*59*60;
PROD3(61) mod 61;
![]()
![]()
>
The two outer products are of course congruent mod 61 (both are 47), but here the inner set of residues has a mod 61 product that is
minus
the other products:
![]() (mod 61). Again, of course, all three products are necessarily related via Wilson's thorem:
(mod 61). Again, of course, all three products are necessarily related via Wilson's thorem:
> PROD1(61)*PROD2(61)*PROD3(61) mod 61;
![]()
> mods(PROD1(61)*PROD2(61)*PROD3(61), 61);
![]()
>
The point now is this :
The question then is this : for which primes p = 1 (mod 3) does one have the middle set of residues (beautifully) related to the outer sets of residues? Meaning? Simply this: setting
 := [Product(r,r = 1 .. (p-1)/3)]](images/reduced TCD talk 9th Feb 200565.gif) ,
,
 := [Product(r,r = (p-1)/3+1 .. 2*(p-1)/3)...](images/reduced TCD talk 9th Feb 200566.gif)
(the
 := [Product(r,r = 2*(p-1)/3+1 .. p-1)]](images/reduced TCD talk 9th Feb 200567.gif) is redundant
is redundant
since one automatically has
![]() (mod
p
))
(mod
p
))
for which primes p = 1 (mod 3), then, does one have
![]() (mod
p
) or
(mod
p
) or
![]() (mod
p
)?
(mod
p
)?
I first show the computation of
![]() , together with the entirely redundant computation of
, together with the entirely redundant computation of
![]() . Readers should now appreciate that
none
of the products are actually being calculated (which would in any event only be possible where
small
numbers were concerned, with 'small' meaning up to a couple of million digits!), but rather modular reduction is being used at all stages,
in the spirit
of the following small hand-performed:
. Readers should now appreciate that
none
of the products are actually being calculated (which would in any event only be possible where
small
numbers were concerned, with 'small' meaning up to a couple of million digits!), but rather modular reduction is being used at all stages,
in the spirit
of the following small hand-performed:
Earlier example . Compute the remainder that 7*8*9*10*11*12 leaves on division by 19.
Solution (note Maple doesn't have congruence notation available for 'Insert Standard Math' work), and so suitably interpret ' = ', sometimes as 'equals', but sometimes as 'is congruent to' in each of the following).
[in normal form; i.e. with remainders between 0 and 18]:
7*8 = 56 = 18 (mod 19)
7*8*9 = 18*9 = 162 = 10 (mod 19)
7*8*9*10 = 10*10 = 100 = 5 (mod 19)
7*8*9*10*11 = 5*11 = 55 = 17 (mod 19)
7*8*9*10*11*12 = 17*12 = 204 = 14 (mod 19)
[in least absolute form; i.e. with remainders between
![]() and 9]:
and 9]:
7*8 = 56 = -1 (mod 19)
7*8*9 = (-1)*9 = -9 (mod 19)
7*8*9*10 = (-9)*10 = -90 = 5 (mod 19)
7*8*9*10*11 = 5*11 = 55 = -2 (mod 19)
7*8*9*10*11*12 = (-2)*12 = -24 = -5 (mod 19)
All those recursive step-by-step modular reductions are captured in the following P[1, 3] and P[2, 3] procedures with the use of:
r := mods(r*k, p)
>
P[1,3] := proc(p) local r, k; r := 1;
for k from 2 to (p-1)/3 do
r := mods(r*k, p) od; r; end:
>
P[2,3] := proc(p) local r, k; r := (p+2)/3;
for k from (p+5)/3 to 2*(p-1)/3 do
r := mods(r*k, p) od; r; end:
>
count:= 0: for k from 2 to 25 do
if ithprime(k) mod 3 = 1
then count := count+1:
p[count] := ithprime(k):
fi; od;
array([[p, `1st set product mod p`, `middle set product mod p`],
seq([p[k], P[1,3](p[k]), P[2,3](p[k])], k=1..count)]);

>
There I tested the first twenty-four odd primes (of which eleven were 1 mod 3), and we found by eye inspection only two instances of what we are looking for: p = 7 and p = 61.
Now I dispense with eye-inspection and use the ' if...fi ' to select only those we are looking for:
>
count:= 0: for k from 2 to 1001 do
if (ithprime(k) mod 3 = 1
and mods(P[1,3](ithprime(k)), ithprime(k))
= P[2,3](ithprime(k)))
or (ithprime(k) mod 3 = 1
and mods(P[1,3](ithprime(k)), ithprime(k))
= -P[2,3](ithprime(k)))
then count := count+1:
p[count] := ithprime(k):
fi; od;
array([[p, `1st set product mod p`, `middle set product mod p`],
seq([p[k], P[1,3](p[k]), P[2,3](p[k])], k=1..count)]);

>
The first one-thousand odd primes were tested there. Of those, exactly 491 are 1 mod 3, and of those exactly 9 primes are of the desired kind, of which we notice that none produce congruent products; we found instances only of the mod p products being the negatives of each other.
Now, I dispense - as we may, for reasons I'll quickly explain - with the redundant computation of the
![]() :
:
since
![]() and
and
![]() are related via Wilson's theorem:
are related via Wilson's theorem:
![]() (mod
p
)
(mod
p
)
then it immediately follows that
Thus, from now on, we are concerned with the following question : for which primes p = 1 (mod 3) does one have:
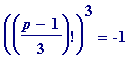 (mod
p
) ... #1 congruence
(mod
p
) ... #1 congruence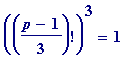 (mod
p
) ... #2 congruence
(mod
p
) ... #2 congruence
That was the question I asked myself several years ago. Actually at that time I only looked for examples of simpler versions of #1 and #2: it is automatic that
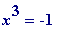 (mod
p
) then
either
x
= -1 (mod
p
)
or
(mod
p
) then
either
x
= -1 (mod
p
)
or
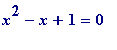 (mod
p
)
(mod
p
)
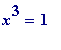 (mod
p
) then
either
x
= 1 (mod
p
)
or
(mod
p
) then
either
x
= 1 (mod
p
)
or
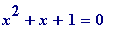 (mod
p)
(mod
p)
and, in fact, at that time I had only investigated possible instances of
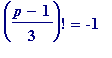 (mod
p
) ... #1' congruence
(mod
p
) ... #1' congruence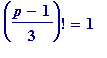 (mod
p
) ... #2' congruence
(mod
p
) ... #2' congruence
At the time, years ago, I noticed a certain something (that I will relate in a moment), but couldn't see anything else, and I dropped it... When I returned to this last November 23rd 2004, I initially investigated as before only #1' and #2' (noticing something that had eluded me all those years ago), and then looked at the wider #1 and #2, noticing there the same phenomena that I had since spotted with #1' and #2'. In the following, then, I am leaping ahead to the investigation of #1 and #2 together:
> restart;
>
P[1,3] := proc(p) local r, k; r := 1;
for k from 2 to (p-1)/3 do
r := mods(r*k, p) od; r; end:
In the following I am searching amongst the first 1000 odd primes for those that are 1 mod 3, and for which either of congruences #1 or #2 are satisfied. The first column
shows the sought
p
's, while the
second column displays the value of the corresponding
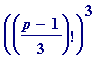 mod
p
, and in the third column is the value of
mod
p
, and in the third column is the value of
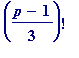 mod
p
:
mod
p
:
>
count:= 0: for k from 2 to 1001 do
if (ithprime(k) mod 3 = 1
and mods(P[1,3](ithprime(k))^3, ithprime(k)) = -1)
or (ithprime(k) mod 3 = 1
and P[1,3](ithprime(k))^3 mod ithprime(k) = 1)
then count := count+1: p[count] := ithprime(k):
fi; od; array([[p,`((p-1)/3)!^3 (p)`, `((p-1)/3)! (p)`],
seq([p[k], P[1,3](p[k])^3 mod p[k], P[1,3](p[k]) mod p[k]], k=1..count)]);
![matrix([[p, `((p-1)/3)!^3 (p)`, `((p-1)/3)! (p)`], ...](images/reduced TCD talk 9th Feb 200594.gif)
>
Since the above computation - which repeats an earlier one - will be done 'live' in my talk you see only the output up to the 1000th odd prime. And what does one notice? Well
But what are those produced p 's? Can one predict some more of them?
Aside
. On Nov 25th 2004 I looked up Sloane's On-Line Encyclopaedia returns for all the primes {
p
} I had at that stage for which #2' held (i.e., those for which
 (mod
p
), and received the following reply:
(mod
p
), and received the following reply:
" I am sorry, but the terms 3571, 4219, 13669, 25117, 55897, 89269, 102121, 170647, 231019, 246247, 251431, 347821 : do not match anything in the table... " (which was of some relief to me, as it gave me some indication that perhaps I was onto something new; how often in the past had I visited Sloane's site thinking I had some new sequence, only to find that... . Later I tried Sloane's site for all the other sequences that I came upon, and none were registered there. [end of aside]
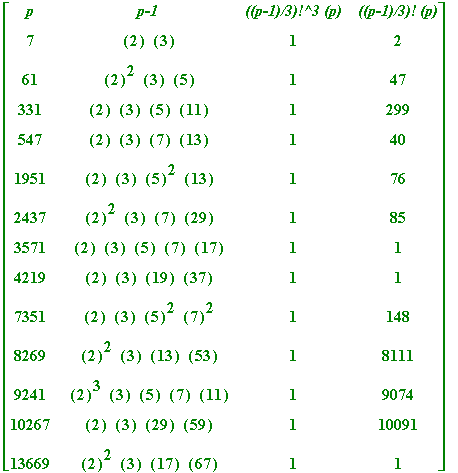
The start of predictions
. Several years ago I had the wit to examine the
prime factorisation
of the corresponding (
![]() ), as I show in the next table, in which I test a bit further (time constraints dictate that I don't go up too high, just the first 1650 odd primes, 815 of which are 1 mod 3):
), as I show in the next table, in which I test a bit further (time constraints dictate that I don't go up too high, just the first 1650 odd primes, 815 of which are 1 mod 3):
>
count:= 0: for k from 2 to 1651 do
if (ithprime(k) mod 3 = 1
and mods(P[1,3](ithprime(k))^3, ithprime(k)) = -1)
or (ithprime(k) mod 3 = 1
and P[1,3](ithprime(k))^3 mod ithprime(k) = 1)
then count := count+1: p[count] := ithprime(k):
fi; od; array([[p,`p-1`,`((p-1)/3)!^3 (p)`, `((p-1)/3)! (p)`],
seq([p[k], ifactor(p[k]-1), P[1,3](p[k])^3 mod p[k], P[1,3](p[k]) mod p[k]], k=1..count)]);
>
What does one notice?
Notice, though, reading backwards through the table that
nothing appears
to be going on
in the cases where
p
= 9241, 7351 (unless you decide to notice, for example, that
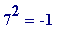 (mod
(mod
![]() )), 3571, ...
)), 3571, ...
I returned to all of this last November 23rd, 2004. I quote exactly from my diary of that day:
"
I also did some (
renewed
) Maple work on 'Wilson 3' - the
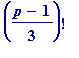 mod p etc. Of course I noticed certain things: the +/-1 residue from the lesser prime, BUT it was only as I was about to go to bed that I
noticed
the:
mod p etc. Of course I noticed certain things: the +/-1 residue from the lesser prime, BUT it was only as I was about to go to bed that I
noticed
the:
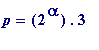 .q.q' + 1 with q' = +/-1 was
really
TIED to the
.q.q' + 1 with q' = +/-1 was
really
TIED to the
![]() ...
"
...
"
Meaning? It jumped out at me that the q' and q (in cases where they were the only primes besides the automatically occurring '2' and '3') weren't just apparently related by some vague congruence, but it seemed that the corresponding congruence had a very precise quotient:
the exact power of 2 occurring in the prime factorisation of
(
![]() )...
)...
Thus, for example, to take the last prime in the above table:
it's not merely
that 67 = -1 (mod 17),
but
in fact
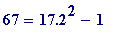 . This deserves a new section:
. This deserves a new section: